* Definición de árbol
* Formas de representación
* Nomenclatura sobre árboles
* Declaración de árbol binario
* Recorridos sobre árboles binarios
* Construcción de un árbol binario
* Árbol binario de búsqueda
* Problemas

Definición de árbol

Un árbol es una estructura de datos, que puede definirse de forma recursiva como:

- Una estructura vacía o
- Un elemento o clave de información (nodo) más un número finito de estructuras tipo árbol, disjuntos, llamados subárboles. Si dicho número de estructuras es inferior o igual a 2, se tiene un árbol binario.

Es, por tanto, una estructura no secuencial.

Otra definición nos da el árbol como un tipo de grafo (ver grafos): un árbol es un grafo acíclico, conexo y no dirigido. Es decir, es un grafo no dirigido en el que existe exactamente un camino entre todo par de nodos. Esta definición permite implementar un árbol y sus operaciones empleando las representaciones que se utilizan para los grafos. Sin embargo, en esta sección no se tratará esta implementación.

Formas de representación

- Mediante un grafo:

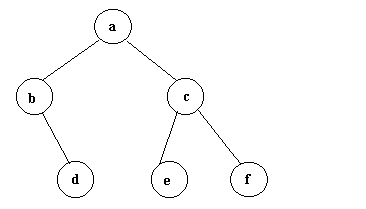
  Figura 1

- Mediante un diagrama encolumnado:

a
  b
    d
  c
    e
    f

En la computación se utiliza mucho una estructura de datos, que son los árboles binarios. Estos árboles tienen 0, 1 ó 2 descendientes como máximo. El árbol de la figura anterior es un ejemplo válido de árbol binario.

Nomenclatura sobre árboles

- Raíz: es aquel elemento que no tiene antecesor; ejemplo: a.
- Rama: arista entre dos nodos.
- Antecesor: un nodo X es es antecesor de un nodo Y si por alguna de las ramas de X se puede llegar a Y.
- Sucesor: un nodo X es sucesor de un nodo Y si por alguna de las ramas de Y se puede llegar a X.
- Grado de un nodo: el número de descendientes directos que tiene. Ejemplo: c tiene grado 2, d tiene grado 0, a tiene grado 2.
- Hoja: nodo que no tiene descendientes: grado 0. Ejemplo: d
- Nodo interno: aquel que tiene al menos un descendiente.
- Nivel: número de ramas que hay que recorrer para llegar de la raíz a un nodo. Ejemplo: el nivel del nodo a es 1 (es un convenio), el nivel del nodo e es 3.
- Altura: el nivel más alto del árbol. En el ejemplo de la figura 1 la altura es 3.
- Anchura: es el mayor valor del número de nodos que hay en un nivel. En la figura, la anchura es 3.

Aclaraciones: se ha denominado a a la raíz, pero se puede observar según la figura que cualquier nodo podría ser considerado raíz, basta con girar el árbol. Podría determinarse por ejemplo que b fuera la raíz, y a y d los sucesores inmediatos de la raíz b. Sin embargo, en las implementaciones sobre un computador que se realizan a continuación es necesaria una jerarquía, es decir, que haya una única raíz.

Declaración de árbol binario

Se definirá el árbol con una clave de tipo entero (puede ser cualquier otra tipo de datos) y dos hijos: izquierdo (izq) y derecho (der). Para representar los enlaces con los hijos se utilizan punteros. El árbol vacío se representará con un puntero nulo.

Un árbol binario puede declararse de la siguiente manera:

Type
  tArbol = ^tNodo;
  tNodo = RECORD
    Clave : Integer;
    Izq, Der : tArbol;
  end;

Otras declaraciones también añaden un enlace al nodo padre, pero no se estudiarán aquí.

Recorridos sobre árboles binarios

Se consideran dos tipos de recorrido: recorrido en profundidad y recorrido en anchura o a nivel. Puesto que los árboles no son secuenciales como las listas, hay que buscar estrategias alternativas para visitar todos los nodos.

- Recorridos en profundidad:

* Recorrido en preorden: consiste en visitar el nodo actual (visitar puede ser simplemente mostrar la clave del nodo por pantalla), y después visitar el subárbol izquierdo y una vez visitado, visitar el subárbol derecho. Es un proceso recursivo por naturaleza.
Si se hace el recorrido en preorden del árbol de la figura 1 las visitas serían en el orden siguiente: a,b,d,c,e,f.

Procedure preorden(a : tarbol);
begin
  if (a <> NIL) then begin
    visitar(a);
    preorden(a^.Izq);
    preorden(a^.Der)
  end
end;

* Recorrido en inorden u orden central: se visita el subárbol izquierdo, el nodo actual, y después se visita el subárbol derecho. En el ejemplo de la figura 1 las visitas serían en este orden: b,d,a,e,c,f.

Procedure inorden(a : tarbol);
begin
  if (a <> NIL) then begin
    inorden(a^.Izq);
    visitar(a);
    inorden(a^.Der)
  end
end;

* Recorrido en postorden: se visitan primero el subárbol izquierdo, después el subárbol derecho, y por último el nodo actual. En el ejemplo de la figura 1 el recorrido quedaría así: d,b,e,f,c,a.

Procedure postorden(a : tarbol);
begin
  if (a <> NIL) then begin
    postorden(a^.Izq);
    postorden(a^.Der)
    visitar(a);
  end
end;

La ventaja del recorrido en postorden es que permite borrar el árbol de forma consistente. Es decir, si visitar se traduce por borrar el nodo actual, al ejecutar este recorrido se borrará el árbol o subárbol que se pasa como parámetro. La razón para hacer esto es que no se debe borrar un nodo y después sus subárboles, porque al borrarlo se pueden perder los enlaces, y aunque no se perdieran se rompe con la regla de manipular una estructura de datos inexistente. Una alternativa es utilizar una variable auxiliar, pero es innecesario aplicando este recorrido.

- Recorrido en amplitud:

Consiste en ir visitando el árbol por niveles. Primero se visitan los nodos de nivel 1 (como mucho hay uno, la raíz), después los nodos de nivel 2, así hasta que ya no queden más.
Si se hace el recorrido en amplitud del árbol de la figura una visitaría los nodos en este orden: a,b,c,d,e,f
En este caso el recorrido no se realizará de forma recursiva sino iterativa, utilizando una cola (ver Colas) como estructura de datos auxiliar. El procedimiento consiste en encolar (si no están vacíos) los subárboles izquierdo y derecho del nodo extraido de la cola, y seguir desencolando y encolando hasta que la cola esté vacía.
En la codificación que viene a continuación no se implementan las operaciones sobre colas.

procedure amplitud(a : tArbol);
var
  cola : tCola;  { las claves de la cola serán de tipo árbol binario }
  aux : tArbol;
  
begin
  if a <> NIL then begin
    CrearCola(cola);
    encolar(cola, a);
    While Not colavacia(cola) Do begin
      desencolar(cola, aux);
      visitar(aux);
      if aux^.izq <> NIL encolar(cola, aux^.izq);
      if aux^.der <> NIL encolar(cola, aux^.der)
    end
  end
end;

Por último, considérese la sustitución de la cola por una pila en el recorrido en amplitud. ¿Qué tipo de recorrido se obtiene?

Construcción de un árbol binario

Hasta el momento se ha visto la declaración y recorrido de un árbol binario. Sin embargo no se ha estudiado ningún método para crearlos. A continuación se estudia un método para crear un árbol binario que no tenga claves repetidas partiendo de su recorrido en preorden e inorden, almacenados en sendos arrays.

Antes de explicarlo se recomienda al lector que lo intente hacer por su cuenta, es sencillo cuando uno es capaz de construir el árbol viendo sus recorridos pero sin haber visto el árbol terminado.

Partiendo de los recorridos preorden e inorden del árbol de la figura 1 puede determinarse que la raíz es el primer elemento del recorrido en preorden. Ese elemento se busca en el array inorden. Los elementos en el array inorden entre izq y la raíz forman el subárbol izquierdo. Asimismo los elementos entre der y la raíz forman el subárbol derecho. Por tanto se tiene este árbol:

A continuación comienza un proceso recursivo. Se procede a crear el subárbol izquierdo, cuyo tamaño está limitado por los índices izq y der. La siguiente posición en el recorrido en preorden es la raíz de este subárbol. Queda esto:

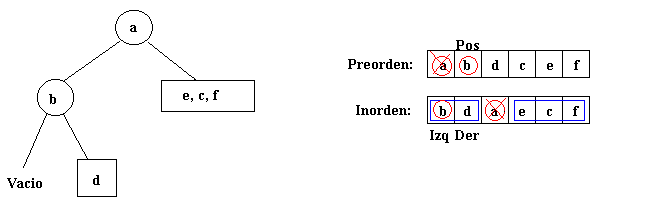
El subárbol b tiene un subárbol derecho, que no tiene ningún descendiente, tal y como indican los índices izq y der. Se ha obtenido el subárbol izquierdo completo de la raíz a, puesto que b no tiene subárbol izquierdo:

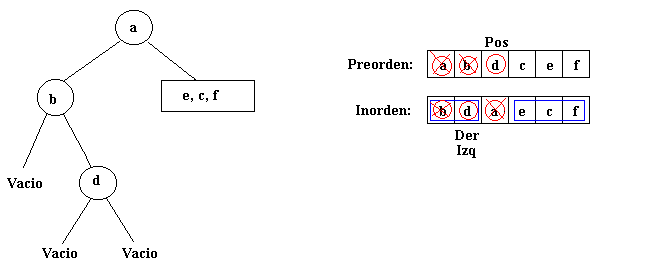
Después seguirá construyéndose el subárbol derecho a partir de la raíz a.

La implementación de la construcción de un árbol partiendo de los recorridos en preorden y en inorden puede consultarse aquí (en C).

Árbol binario de búsqueda

Un árbol binario de búsqueda es aquel que es:

- Una estructura vacía o
- Un elemento o clave de información (nodo) más un número finito -a lo sumo dos- de estructuras tipo árbol, disjuntos, llamados subárboles y además cumplen lo siguiente:

  * Todas las claves del subárbol izquierdo al nodo son menores que la clave del nodo.
  * Todas las claves del subárbol derecho al nodo son mayores que la clave del nodo.
  * Ambos subárboles son árboles binarios de búsqueda.

Un ejemplo de árbol binario de búsqueda:

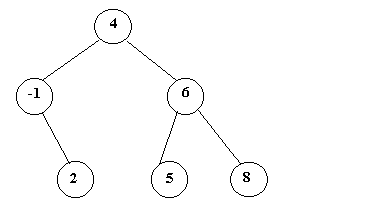
Figura 5

Al definir el tipo de datos que representa la clave de un nodo dentro de un árbol binario de búsqueda es necesario que en dicho tipo se pueda establecer una relación de orden. Por ejemplo, suponer que el tipo de datos de la clave es un puntero (da igual a lo que apunte). Si se codifica el árbol en Pascal no se puede establecer una relación de orden para las claves, puesto que Pascal no admite determinar si un puntero es mayor o menor que otro.

En el ejemplo de la figura 5 las claves son números enteros. Dada la raíz 4, las claves del subárbol izquierdo son menores que 4, y las claves del subárbol derecho son mayores que 4. Esto se cumple también para todos los subárboles. Si se hace el recorrido de este árbol en orden central se obtiene una lista de los números ordenada de menor a mayor.
Cuestión: ¿Qué hay que hacer para obtener una lista de los números ordenada de mayor a menor?

Una ventaja fundamental de los árboles de búsqueda es que son en general mucho más rápidos para localizar un elemento que una lista enlazada. Por tanto, son más rápidos para insertar y borrar elementos. Si el árbol está perfectamente equilibrado -esto es, la diferencia entre el número de nodos del subárbol izquierdo y el número de nodos del subárbol derecho es a lo sumo 1, para todos los nodos- entonces el número de comparaciones necesarias para localizar una clave es aproximadamente de logN en el peor caso. Además, el algoritmo de inserción en un árbol binario de búsqueda tiene la ventaja -sobre los arrays ordenados, donde se emplearía búsqueda dicotómica para localizar un elemento- de que no necesita hacer una reubicación de los elementos de la estructura para que esta siga ordenada después de la inserción. Dicho algoritmo funciona avanzando por el árbol escogiendo la rama izquierda o derecha en función de la clave que se inserta y la clave del nodo actual, hasta encontrar su ubicación; por ejemplo, insertar la clave 7 en el árbol de la figura 5 requiere avanzar por el árbol hasta llegar a la clave 8, e introducir la nueva clave en el subárbol izquierdo a 8.
El algoritmo de borrado en árboles es algo más complejo, pero más eficiente que el de borrado en un array ordenado.

Ahora bien, suponer que se tiene un árbol vacío, que admite claves de tipo entero. Suponer que se van a ir introduciendo las claves de forma ascendente. Ejemplo: 1,2,3,4,5,6
Se crea un árbol cuya raíz tiene la clave 1. Se inserta la clave 2 en el subárbol derecho de 1. A continuación se inserta la clave 3 en el subárbol derecho de 2.
Continuando las inserciones se ve que el árbol degenera en una lista secuencial, reduciendo drásticamente su eficacia para localizar un elemento. De todas formas es poco probable que se de un caso de este tipo en la práctica. Si las claves a introducir llegan de forma más o menos aleatoria entonces la implementación de operaciones sobre un árbol binario de búsqueda que vienen a continuación son en general suficientes.

Existen variaciones sobre estos árboles, como los AVL o Red-Black (no se tratan aquí), que sin llegar a cumplir al 100% el criterio de árbol perfectamente equilibrado, evitan problemas como el de obtener una lista degenerada.

Operaciones básicas sobre árboles binarios de búsqueda

- Búsqueda

Si el árbol no es de búsqueda, es necesario emplear uno de los recorridos anteriores sobre el árbol para localizarlo. El resultado es idéntico al de una búsqueda secuencial. Aprovechando las propiedades del árbol de búsqueda se puede acelerar la localización. Simplemente hay que descender a lo largo del árbol a izquierda o derecha dependiendo del elemento que se busca.

Function buscar(a : tarbol; elem : Integer) : boolean;
begin
  if a = NIL then buscar := FALSE
  else if a^.clave < elem then buscar := buscar(a^.der, elem)
  else if a^.clave > elem then buscar := buscar(a^.izq, elem)
  else buscar := TRUE
end;

- Inserción

La inserción tampoco es complicada. Es más, resulta practicamente idéntica a la búsqueda. Cuando se llega a un árbol vacío se crea el nodo en el puntero que se pasa como parámetro por referencia, de esta manera los nuevos enlaces mantienen la coherencia. Si el elemento a insertar ya existe entonces no se hace nada.

Procedure insertar(var a :tarbol; elem : Integer);
begin
  if a = NIL then begin
    new(a);
    a^.clave := elem;
    a^.izq := NIL;
    a^.der := NIL;
  end
  else if a^.clave < elem then insertar(a^.der, elem)
  else if a^.clave > elem then insertar(a^.izq, elem)
end;

- Borrado

La operación de borrado si resulta ser algo más complicada. Se recuerda que el árbol debe seguir siendo de búsqueda tras el borrado. Pueden darse tres casos, una vez encontrado el nodo a borrar:
1) El nodo no tiene descendientes. Simplemente se borra.
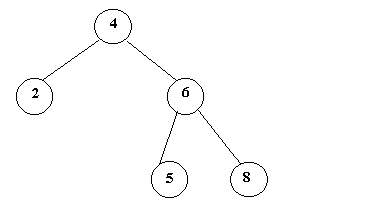
2) El nodo tiene al menos un descendiente por una sola rama. Se borra dicho nodo, y su primer descendiente se asigna como hijo del padre del nodo borrado. Ejemplo: en el árbol de la figura 5 se borra el nodo cuya clave es -1. El árbol resultante es:

3) El nodo tiene al menos un descendiente por cada rama. Al borrar dicho nodo es necesario mantener la coherencia de los enlaces, además de seguir manteniendo la estructura como un árbol binario de búsqueda. La solución consiste en sustituir la información del nodo que se borra por el de una de las hojas, y borrar a continuación dicha hoja. ¿Puede ser cualquier hoja? No, debe ser la que contenga una de estas dos claves:
· la mayor de las claves menores al nodo que se borra. Suponer que se quiere borrar el nodo 4 del árbol de la figura 5. Se sustituirá la clave 4 por la clave 2.
· la menor de las claves mayores al nodo que se borra. Suponer que se quiere borrar el nodo 4 del árbol de la figura 5. Se sustituirá la clave 4 por la clave 5.

El algoritmo de borrado que se implementa a continuación realiza la sustitución por la mayor de las claves menores, (aunque se puede escoger la otra opción sin pérdida de generalidad). Para lograr esto es necesario descender primero a la izquierda del nodo que se va a borrar, y después avanzar siempre a la derecha hasta encontrar un nodo hoja. A continuación se muestra gráficamente el proceso de borrar el nodo de clave 4:

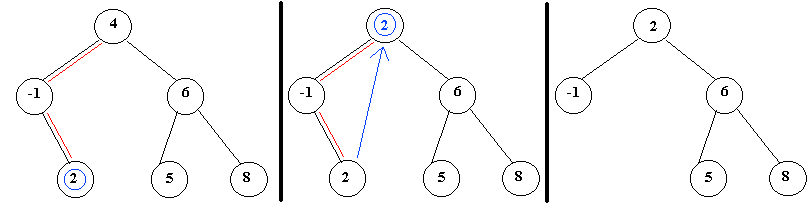
Codificación: el procedimiento sustituir es el que desciende por el árbol cuando se da el caso del nodo con descencientes por ambas ramas.

Procedure Borrar(var a : tarbol; elem : Integer);
Var
   aux : tarbol;

  Procedure sustituir(Var b : tarbol);
  begin
    if b^.der <> NIL then sustituir(b^.der)
    else begin
     aux^.clave := b^.clave;
     aux := b;
     b := b^.izq;
    end
  end;

begin

  if a = NIL then exit	{ No existe la clave }

  else if a^.clave < elem then borrar(a^.der, elem)
  else if a^.clave > elem then borrar(a^.izq, elem)
  else begin
    aux := a;
    if a^.izq = NIL then a := a^.der
    else if a^.der = NIL then a := a^.izq
    else sustituir(a^.izq); { se sustituye por la mayor de las menores }
    dispose(aux)
  end
end;

Ejercicio resuelto

Escribir una función que devuelva el numero de nodos de un árbol binario. Una solución recursiva puede ser la siguiente:

funcion nodos(arbol : tipoArbol) : devuelve entero;
inicio
 si arbol = vacio entonces devolver 0;
 en otro caso devolver (1 + nodos(subarbol_izq) + nodos(subarbol_der));
fin

Adaptarlo para que detecte si un árbol es perfectamente equilibrado o no.

Problemas propuestos

Árboles binarios: OIE 98. (Enunciado)

Aplicación práctica de un árbol

Se tiene un fichero de texto ASCII. Para este propósito puede servir cualquier libro electrónico de la librería Gutenberg o Cervantes, que suelen tener varios cientos de miles de palabras. El objetivo es clasificar todas las palabras, es decir, determinar que palabras aparecen, y cuantas veces aparece cada una. Palabras como 'niño'-'niña', 'vengo'-'vienes' etc, se consideran diferentes por simplificar el problema.

Escribir un programa, que recibiendo como entrada un texto, realice la clasificación descrita anteriormente.
Ejemplo:
Texto: "a b'a c. hola, adios, hola"

La salida que produce es la siguiente:
a 2
adios 1
b 1
c 1
hola 2

Nótese que el empleo de una lista enlazada ordenada no es una buena solución. Si se obtienen hasta 20.000 palabras diferentes, por decir un número, localizar una palabra cualquiera puede ser, y en general lo será, muy costoso en tiempo. Se puede hacer una implementación por pura curiosidad para evaluar el tiempo de ejecución, pero no merece la pena.

La solución pasa por emplear un árbol binario de búsqueda para insertar las claves. El valor de log(20.000) es aproximadamente de 14. Eso quiere decir que localizar una palabra entre 20.000 llevaría en el peor caso unos 14 accesos. El contraste con el empleo de una lista es simplemente abismal. Por supuesto, como se ha comentado anteriormente el árbol no va a estar perfectamente equilibrado, pero nadie escribe novelas manteniendo el orden lexicográfico (como un diccionario) entre las palabras, asi que no se obtendrá nunca un árbol muy degenerado. Lo que está claro es que cualquier evolución del árbol siempre será mejor que el empleo de una lista.

Por último, una vez realizada la lectura de los datos, sólo queda hacer un recorrido en orden central del árbol y se obtendrá la solución pedida en cuestión de segundos.

Una posible definición de la estructura árbol es la siguiente:

Type
  tArbol = ^tNodo;
  tNodo = RECORD
    Clave : String;
    contador : Integer; { numero de apariciones. Iniciar a 0 }
    Izq, Der : tArbol;
  end;