* Introducción
* La vuelta del caballo
* El problema de las ocho reinas
* El problema de la mochila (selección óptima)
* Problemas propuestos
Introducción
Los algoritmos de vuelta atrás se utilizan para encontrar
soluciones a un problema. No siguen unas reglas para la búsqueda de la
solución, simplemente una búsqueda sistemática, que más
o menos viene a significar que hay que probar todo lo posible hasta encontrar
la solución o encontrar que no existe solución al problema. Para
conseguir este propósito, se separa la búsqueda en varias búsquedas
parciales o subtareas. Asimismo, estas subtareas suelen incluir más subtareas,
por lo que el tratamiento general de estos algoritmos es de naturaleza recursiva.
¿Por qué se llaman algoritmos de vuelta atrás?.
Porque en el caso de no encontrar una solución en una subtarea se retrocede
a la subtarea original y se prueba otra cosa distinta (una nueva subtarea distinta
a las probadas anteriormente).
Puesto que a veces nos interesa conocer múltiples soluciones
de un problema, estos algoritmos se pueden modificar fácilmente para
obtener una única solución (si existe) o todas las soluciones
posibles (si existe más de una) al problema dado.
Estos algoritmos se asemejan al recorrido en profundidad dentro
de un grafo (ver sección de grafos, estructuras de datos, y recorrido
de grafos, algoritmos), siendo cada subtarea un nodo del grafo. El caso es que
el grafo no está definido de forma explícita (como lista o matriz
de adyacencia), sino de forma implícita, es decir, que se irá
creando según avance el recorrido. A menudo dicho grafo es un árbol,
o no contiene ciclos, es decir, al buscar una solución es, en general,
imposible llegar a una misma solución x partiendo de dos subtareas
distintas a y b; o de la subtarea a es imposible llegar
a la subtaréa b y viceversa.
Gráficamente se puede ver así:
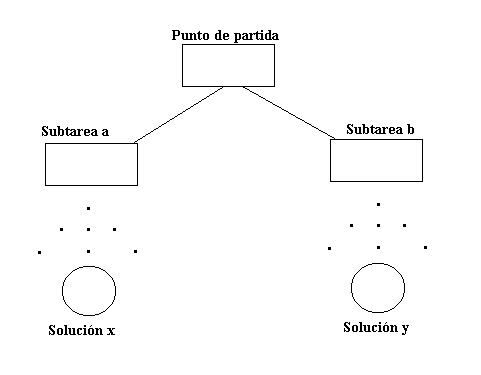
A menudo ocurre que el árbol o grafo que se genera es
tan grande que encontrar una solución o encontrar la mejor solución
entre varias posibles es computacionalmente muy costoso. En estos casos suelen
aplicarse una serie de restricciones, de tal forma que se puedan podar
algunas de las ramas, es decir, no recorrer ciertas subtareas. Esto es posible
si llegado a un punto se puede demostrar que la solución que se obtendrá
a partir de ese punto no será mejor que la mejor solución obtenida
hasta el momento. Si se hace correctamente, la poda no impide encontrar la mejor
solución.
A veces, es imposible demostrar que al hacer una poda no se esté
ocultando una buena solución. Sin embargo, el problema quizás
no pida la mejor solución, sino una que sea razonablemente buena y cuyo
coste computacional sea bastante reducido. Esa es una buena razón para
aumentar las restricciones a la hora de recorrer un nodo. Tal vez se pierda
la mejor solución, pero se encontrará una aceptable en un tiempo
reducido.
Los algoritmos de vuelta atrás tienen un esquema genérico,
según se busque una o todas las soluciones, y puede adaptarse fácilmente
según las necesidades de cada problema. A continuación se exponen
estos esquemas, extraídos de Wirth (ver Bibliografía).
Los bloques se agrupan con begin y end, equivalentes a los corchetes
de C, además están tabulados.
- esquema para una solución:
procedimiento ensayar (paso : TipoPaso)
repetir
| seleccionar_candidato
| if aceptable then
| begin
| anotar_candidato
| if solucion_incompleta then
| begin
| ensayar(paso_siguiente)
| if no acertado
then borrar_candidato
| end
| else begin
| anotar_solucion
| acertado <- cierto;
| end
hasta que (acertado = cierto) o (candidatos_agotados)
fin procedimiento
- esquema para todas las soluciones:
procedimiento ensayar
(paso : TipoPaso)
para cada candidato hacer
| seleccionar candidato
| if aceptable then
| begin
| anotar_candidato
| if solucion_incompleta then
| ensayar(paso_siguiente)
| else
|
almacenar_solucion
| borrar_candidato
| end
hasta que candidatos_agotados
fin procedimiento
Por último, se exponen una serie de problemas típicos
que se pueden resolver fácilmente con las técnicas de vuelta atrás.
El primero que se expone es muy conocido. Se trata de la vuelta del caballo.
Muchos problemas de los pasatiempos de los periódicos pueden resolverse
con la ayuda de un ordenador y en esta web se muestran algunos de ellos.
La vuelta del caballo
Se dispone de un tablero rectangular, por ejemplo el tablero
de ajedrez, y de un caballo, que se mueve según las reglas de este juego.
El objetivo es encontrar una manera de recorrer todo el tablero partiendo de
una casilla determinada, de tal forma que el caballo pase una sola vez por cada
casilla. Una variante es obligar al caballo a volver a la posición de
partida en el último movimiento.
Por último se estudiará como encontrar todas las soluciones posibles
partiendo de una misma casilla.
Para resolver el problema hay que realizar todos los movimientos
posibles hasta que ya no se pueda avanzar, en cuyo caso hay que dar marcha atrás,
o bien hasta que se cubra el tablero. Además, es necesario determinar
la organización de los datos para implementar el algoritmo.
- ¿Cómo se mueve un caballo?. Para aquellos que
no sepan jugar al ajedrez se muestra un gráfico con los ocho movimientos
que puede realizar. Estos movimientos serán los ocho candidatos.
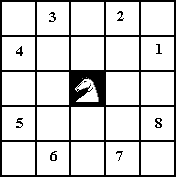
Con las coordenadas en las que se encuentre el caballo y las
ocho coordenadas relativas se determina el siguiente movimiento. Las coordenas
relativas se guardan en dos arrays:
ejex = [2, 1, -1, -2, -2, -1, 1, 2]
ejey = [1, 2, 2, 1, -1, -2, -2, -1]
El tablero, del tamaño que sea, se representará
mediante un array bidimensional de números enteros. A continuación
se muestra un gráfico con un tablero de tamaño 5x5 con todo el
recorrido partiendo de la esquina superior izquierda.
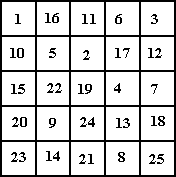
Cuando se encuentra una solución, una variable que se
pasa por referencia es puesta a 1 (cierto). Puede hacerse una variable de alcance
global y simplificar un poco el código, pero esto no siempre es recomendable.
Para codificar el programa, es necesario considerar algunos aspectos
más, entre otras cosas no salirse de los límites del tablero y
no pisar una casilla ya cubierta (selección del candidato). Se determina
que hay solución cuando ya no hay más casillas que recorrer.
A continuación se expone un código completo en
C, que recubre un tablero cuadrado de lado N partiendo de la posición
(0,0).
#include <stdio.h>
#define N 5
#define ncuad N*N
void mover(int tablero[][N], int i, int pos_x, int pos_y, int *q);
const int ejex[8] = { -1,-2,-2,-1, 1, 2, 2, 1 },
ejey[8] = { -2,-1, 1, 2, 2, 1,-1,-2 };
int main(void)
{
int tablero[N][N]; /* tablero del caballo. */
int i,j,q;
/* inicializa el tablero a cero */
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
tablero[i][j] = 0;
/* pone el primer movimiento */
tablero[0][0] = 1;
mover(tablero,2,0,0,&q);
if (q) { /* hay solucion: la muestra. */
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
printf("%3d ", tablero[i][j]);
putchar('\n');
}
}
else
printf("\nNo existe solucion\n");
return 0;
}
void mover(int tablero[][N],int i, int pos_x, int pos_y, int *q)
{
int k, u, v;
k = 0;
*q = 0;
do {
u = pos_x + ejex[k]; v = pos_y + ejey[k]; /* seleccionar candidato */
if (u >= 0 && u < N && v >= 0 && v < N) { /* esta dentro de los limites? */
if (tablero[u][v] == 0) { /* es valido? */
tablero[u][v] = i; /* anota el candidato */
if (i < ncuad) { /* llega al final del recorrido? */
mover(tablero,i+1,u,v,q);
if (!*q) tablero[u][v] = 0; /* borra el candidato */
}
else *q = 1; /* hay solucion */
}
}
k++;
} while (!*q && k < 8);
}
Cambiando el valor de N puede
obtenerse una solución para un tablero cuadrado de tamaño N.
A continuación, se muestra
una adaptación del procedimiento que muestra todas las soluciones. Si
se ejecuta para N = 5 se encuentra que hay 304 soluciones partiendo de la esquina
superior izquierda.
Cuando se encuentra una solución se llama a un procedimiento (no se ha
codificado aquí) que imprime todo el tablero.
void mover(int tablero[][N],int
i, int pos_x, int pos_y)
{
int k, u, v;
for (k = 0; k < 8; k++) {
u = pos_x + ejex[k]; v = pos_y + ejey[k];
if (u >= 0 && u < N && v >=
0 && v < N) { /* esta dentro de los limites */
if (tablero[u][v] == 0) {
tablero[u][v] = i;
if (i < ncuad)
mover(tablero,i+1,u,v);
else imprimir_solucion(tablero);
tablero[u][v] = 0;
}
}
}
}
El problema de las ocho reinas
Continuamos con problemas relacionados
con el ajedrez. El problema que ahora se plantea es claramente, como se verá,
de vuelta atrás. Se recomienda intentar resolverlo a mano.
Se trata de colocar ocho reinas sobre
un tablero de ajedrez, de tal forma que ninguna amenace (pueda comerse) a otra.
Para los que no sepan ajedrez deben saber que una reina amenaza a otra pieza
que esté en la misma columna, fila o cualquiera de las cuatro diagonales.
La dificultad que plantea este problema
es la representación de los datos. Se puede utilizar un array bidimensional
de tamaño 8x8, pero las operaciones para encontrar una reina que amenace
a otra son algo engorrosas y hay un truco para evitarlas. La solución
aquí expuesta vuelve a ser tomada de Wirth (ver
Bibliografía).
Es lógico que cada reina debe
ir en una fila distinta. Por tanto, en un array se guarda la posición
de cada reina en la columna que se encuentre. Ejemplo: si en la tercera fila
hay una reina situada en la quinta columna, entonces la tercera posición
del array guardará un 5. A este array se le llamará col.
Hace falta otro array que determine si hay puesta una reina en la fila j-ésima.
A este array se le llamará fila.
Por último se utilizan dos arrays más para determinar las diagonales
libres, y se llamarán diagb y diagc.
Para poner una reina se utiliza esta
instrucción:
col[i] = j ; fila[j] = diagb[i+j] = diagc[7+i-j] = FALSE;
Para quitar una reina esta otra:
fila[j] = diagb[i+j] = diagc[7+i-j] = TRUE;
Se considera válida la posición para este caso:
if (fila[j] && diagb[i+j] && diagc[7+i-j])
entonces proceder ...
A continuación se expone el
código completo en C. Se han utilizado tipos enumerados para representar
los valores booleanos.
#include <stdio.h>
enum bool {FALSE, TRUE};
typedef enum bool boolean;
void ensayar(int i, boolean *q, int col[], boolean fila[], boolean diagb[], boolean diagc[]);
int main(void)
{
int i;
boolean q;
int col[8];
boolean fila[8],diagb[15], diagc[15];
for (i = 0; i < 8; i++) fila[i] = TRUE;
for (i = 0; i < 15; i++) diagb[i] = diagc[i] = TRUE;
ensayar(0,&q,col,fila,diagb,diagc);
if (q) {
printf("\nSolucion:");
for (i = 0; i < 8; i++) printf(" %d", col[i]);
} else printf("\nNo hay solucion");
return 0;
}
void ensayar(int i, boolean *q, int col[], boolean fila[], boolean diagb[], boolean diagc[])
{
int j;
j = 0;
*q = FALSE;
do {
if (fila[j] && diagb[i+j] && diagc[7+i-j]) {
col[i] = j; fila[j] = diagb[i+j] = diagc[7+i-j] = FALSE;
if (i < 7) { /* encuentra solucion? */
ensayar(i+1,q,col,fila,diagb,diagc);
if (!*q)
fila[j] = diagb[i+j] = diagc[7+i-j] = TRUE;
} else *q = TRUE; /* encuentra la solucion */
}
j++;
} while (!*q && j < 8);
}
Por último, se deja al lector que implemente un procedimiento
que encuentre todas las soluciones. Si se desea complicar más entonces
se puede pedir que encuentre todas las soluciones distintas, es decir, aquellas
que no sean rotaciones o inversiones de otras soluciones.
Ahora que se conoce el método general, puede hacerse extensible
a múltiples piezas simultáneamente.
El Problema de la mochila (selección
óptima)
Con anterioridad se ha estudiado la posibilidad de encontrar
una única solución a un problema y la posibilidad de encontrarlas
todas. Pues bien, ahora se trata de encontrar la mejor solución, la solución
óptima, de entre todas las soluciones.
Partiendo del esquema que genera todas las soluciones expuesto anteriormente
se puede obtener la mejor solución (la solución óptima,
seleccionada entre todas las soluciones) si se modifica la instrucción
almacenar_solucion por esta otra:
si f(solucion)
> f(optimo) entonces optimo <- solucion
siendo f(s) función positiva, optimo es la mejor solucion
encontrada hasta el momento, y solucion es una solucion que se está
probando.
El problema de la mochila consiste en llenar una mochila con
una serie de objetos que tienen una serie de pesos con un valor asociado. Es
decir, se dispone de n tipos de objetos y que no hay un número
limitado de cada tipo de objeto (si fuera limitado no cambia mucho el problema).
Cada tipo i de objeto tiene un peso wi positivo y un
valor vi positivo asociados. La mochila tiene una capacidad de peso
igual a W. Se trata de llenar la mochila de tal manera que se maximice
el valor de los objetos incluidos pero respetando al mismo tiempo la
restricción de capacidad. Notar que no es obligatorio que una solución
óptima llegue al límite de capacidad de la mochila.
Ejemplo: se supondrá:
n = 4
W = 8
w() = 2, 3, 4, 5
v() = 3, 5, 6, 10
Es decir, hay 4 tipos de objetos y la mochila tiene una capacidad de 8. Los
pesos varían entre 2 y 5, y los valores relacionados varían entre
3 y 10.
Una solución no óptima de valor 12 se obtiene introduciendo cuatro
objetos de peso 2, o 2 de peso 4. Otra solución no óptima de valor
13 se obtiene introduciendo 2 objetos de peso 3 y 1 objeto de peso 2. ¿Cuál
es la solución óptima?.
A continuación se muestra una solución al problema,
variante del esquema para obtener todas las soluciones.
void mochila(int i, int r, int solucion, int *optimo)
{
int k;
for (k = i; k < n; k++) {
if (peso[k] <= r) {
mochila(k, r - peso[k], solucion + valor[k], optimo);
if (solucion + valor[k] > *optimo) *optimo = solucion+valor[k];
}
}
}
Dicho procedimiento puede ser ejecutado
de esta manera, siendo n, W,
peso y valor variables
globales para simplificar el programa:
n = 4,
W = 8,
peso[] = {2,3,4,5},
valor[] = {3,5,6,10},
optimo = 0;
...
mochila(0, W, 0, &optimo);
Observar que la solución óptima se obtiene independientemente
de la forma en que se ordenen los objetos.
Problemas propuestos
- Caminos. OIE 97.
Enunciado - Solución
- Tom y Jerry (solamente el apartado 3). OIE 97.
Enunciado
- Buque. OIE 98.
Enunciado
- Sellos (El correo del zar). OIE 99.
Enunciado
- El salto del caballo. OIE 2001.
Enunciado
- Islas en el mar. IOI 92.
Enunciado
(en inglés: Islands in the sea)
- Números primos. IOI 94.
Enunciado
(en inglés: The Primes) - Solución
- Muchos otros problemas requieren vuelta atrás, en general se trata
de algoritmos auxiliares para resolver una pequeña tarea.
- También los algoritmos de vuelta atrás permiten la resolución
del problema del laberinto, puesto que la vuelta atrás no es más
que el recorrido sobre un grafo implícito
finito o infinito. De todas formas, los problemas de laberintos se resuelven
mucho mejor mediante exploración en anchura (ver grafos). |