Se nos pide que comprobemos la trayectoria de un robot en un
recinto rectangular delimitado por cuatro paredes, cada una de ellas orientada
a uno de los puntos cardinales (en sentido horario: N, E, S y O).
El robot está diseñado para desplazarse utilizando
una cuadrícula que cubre el suelo del recinto, de modo que puede avanzar
en cada paso desde una casilla hasta cualquiera de las que tenga un lado en
común con ella. Así, podemos considerar el espacio por el que
puede moverse el robot dividido en m filas (numeradas de 1 a m, yendo de N a
S) y n columnas (numeradas de 1 a n, yendo de O a E).
El robot se desplaza de acuerdo a tres órdenes diferentes:
"giro a la izquierda" (I), "giro a la derecha" (D) y "avance"
(A). El avance se realiza de casilla en casilla (una cada vez), pudiéndose
sólo pasar desde la casilla en la que se encuentre el robot a cada una
de las cuatro (o menos) que tienen un lado en común con esta. En todo
momento el robot está orientado directamente hacia uno de los cuatro
lados de la casilla en la que se encuentra (que distinguiremos nombrándolos
como los puntos cardinales; es decir, en sentido horario: N, E, S y O), y las
órdenes I y D hacen girar al robot 90º sin avanzar. De este modo,
si por ejemplo el robot tiene orientación N, con la orden I, quedaría
en la misma casilla pero con orientación O (pues el giro hacia la izquierda
corresponde al giro antihorario); y con la orden D quedaría orientado
al E (pues el giro a la derecha es el que se realiza en sentido horario). La
orden de avance se aplica siempre en la orientación que tenga en ese
momento el robot y ha de tenerse en cuenta que un intento de avanzar contra
los límites del recinto provocaría la destrucción del robot.
El problema es que el espacio por el que ha de desplazarse el
robot se encuentra minado, de forma que si el robot pisa alguna de las casillas
que tiene una mina será destruido. Lo mismo sucede si el robot se estrella
contra alguna de las paredes del recinto al recibir una orden de avance incorrecta,
como ya hemos dicho.
Los programadores del robot se encargan de generar la secuencia
de órdenes que le harían llegar de su posición inicial
a un destino. Nuestra responsabilidad es la de supervisar esta secuencia propuesta
y asegurarnos que la solución que nos proponen los programadores es correcta
y no supone ningún peligro para la integridad del robot.
Objetivo
Se trata de comprobar que una secuencia de órdenes determinada
desplaza el robot dentro del recinto sin que sea destruido.
Entrada
La entrada del programa consiste de una secuencia de líneas,
que residen en un archivo de texto (ASCII) con nombre ROBCOM.DAT, que tendrá
el siguiente formato:
· La primera línea (la 1) contiene el número de filas (m)
y columnas (n) del recinto separados por una coma y sin espacios en blanco.
Podéis suponer que se cumple 1 <= m < 100 y 1 <= n <
100.
· Las m líneas siguientes (de la 2 a la m+1) contienen, cada una,
una fila del recinto. Concretamente, la línea tendrá n ceros o
unos separados por comas y sin espacios en blanco entre ellos. Un 0 corresponde
a una casilla que puede ser pisada sin peligro y un 1 corresponde a una casilla
minada.
· La siguiente línea (la m+2) contiene las coordenadas (i1, j1),
1 <= i1 <= m, 1 <= j1 <= n, de la posición inicial
del robot, separadas con una coma y sin espacios en blanco.
· La siguiente línea (la m+3) contiene las coordenadas (i2, j2),
1 <= i1 <= m, 1 <= j1 <= n, del destino del robot, separadas
con una coma y sin espacios en blanco.
· La siguiente línea (la m+4) contiene una única letra
indicando la orientación inicial del robot (N, E, S o O).
· La siguiente línea (la m+5) contiene el número de órdenes
dadas al robot (entre 1 y 40).
· La última línea (la m+6) contiene la secuencia de órdenes,
es decir, letras "A", "D" e "I", separadas por
un único blanco y sin blancos al inicio ni al final de la línea.
Salida
La salida del programa ha de grabarse en un archivo de texto
(ASCII) con nombre ROBCOM.RES, y constará de una única letra:
una "C", si la secuencia de órdenes lleva de la posición
inicial al destino sin destruir el robot, o una "E" en caso contrario.
Ejemplo de entrada
4,5
0,1,0,0,0
1,0,1,1,0
0,0,1,0,0
0,0,0,0,0
2,2
1,3
E
16
D A A I A A I A D A I A A I A A
Ejemplo de salida
C
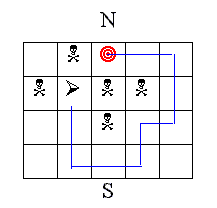
|
| circulo: destino; flecha: robot orientado; calaveras: posiciones
minadas |
|