Existen varios ámbitos de aplicaciones informáticas que manejan el concepto de red topológica. Por ejemplo, cuando se modelizan redes de ordenadores, de carreteras, y similares. Sobre estas redes, nos puede interesar preguntar ciertas cosas: si dos ordenadores están conectados, cuál es el camino más corto para ir de una ciudad a otra, etc. En este problema, nos dirigimos a un problema concreto en este contexto, la búsqueda de subredes interesantes.

Definición

Sea una red R que contiene un conjunto V de elementos (por ejemplo, ordenadores) y un conjunto C de conexiones bidireccionales entre pares de elementos de V. Una subred interesante de R se define como un conjunto W de más de dos elementos tal que W Í V y todo par de elementos de W está conectado por alguna conexión de C.
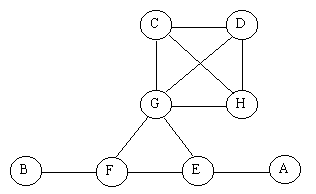
Por ejemplo, en la red que se muestra en la figura siguiente, existe una única subred interesante, que aparece en el centro de la red (uniendo los nodos E, F y G).

Objetivo

Dada una red R, se quiere obtener todas sus subredes interesantes que sean maximales, es decir, que no formen parte de ninguna otra subred interesante.

Entrada

La entrada del programa consiste en una secuencia de líneas, que residen en un archivo de texto (ASCII) con nombre RED.DAT, que tendrá el siguiente formato:

• La primera línea (la 1) contiene el número m de conexiones de la red. Podéis suponer 1 <= m <= 99.
• Las m líneas siguientes contienen, cada una, dos letras mayúsculas (del alfabeto anglosajón, es decir, sin 'Ñ' ni 'Ç' pero con 'W') sin acentos separadas por caracteres "espacio", que representan conexiones entre elementos de la red.
  

Salida

La salida del programa ha de grabarse en un archivo de texto (ASCII) con nombre RED.RES, que contendrá una línea por cada subred interesante maximal que contenga la red, escribiendo los elementos que lo forman en orden alfabético separados por un único carácter "espacio". En la salida, las subredes se ordenan por número de elementos que contienen y, en caso de subredes igual de grandes, no se exige ningún orden adicional.

Ejemplo

Se muestra una entrada que representa una red que contiene dos subredes interesantes maximales. En concreto, nótese que la subred formada por los elementos C, D, G y H contiene otras subredes interesantes pero que, al no ser maximales, no aparecen en el resultado.

Ejemplo de entrada 11 E F F B E A H G C D G E C H F G H D G D C G
Ejemplo de salida C D G H E F G